Comparison between the Second Zagreb Eccentricity Index and Eccentric Connectivity Index of Graphs Volume 1 - Issue 1

Huimin Li¹, Fang Gao¹ and Kexiang Xu ay²*

• ¹College of Science, China
• ²School of Mathematics and Computer Science, China

Received: November 12, 2018;   Published: November 19, 2018

*Corresponding author: Kexiang Xu ay, School of Mathematics and Computer Science, Anhui 247000, PR China

DOI: 10.32474/CTCSA.2018.01.000105

Abstract PDF

Abstract

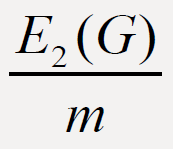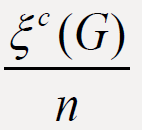For a graph G, the second Zagreb eccentricity index E₂(G) and eccentric connectivity index ∈^c(G) are two eccentricity-based invariants of graph G. In this paper we prove some results on the comparison between and of connected graphs G of order n and with m edges.

The authors demonstrated how a combination of both techniques and human interventions enhances control, decision-making and data analysis systems.

Keywords: Graph; Eccentricity (of vertex); Second Zagreb eccentricity index; Eccentric connectivity index

Introduction

Throughout this paper we only consider the note, undirected, simple and connected graphs. The degree of v∈ V(G), denoted by deg_G(v), is the number of vertices in G adjacent to v. For any two vertices u; v in a graph G, the distance between them, denoted by d_G(u; v), is the length of a shortest path connecting them in G. As usual, let Sn, Pn, Cn, Kn be the star graph, path graph, cycle graph and complete graph, respectively, on n vertices. Other undefined notations and terminology on the graph theory can be found in [1]. For any vertex of graph G, the eccentricity ∈_G (v) (or ∈(v) for short) is the maximum distance from v to other vertices of G, i.e., ∈_G (v)= max_u≠v d_G(u,v). The eccentricity of a vertex is an important parameter in pure graph theory. The radius of a graph G is denoted by r(G) and defined by 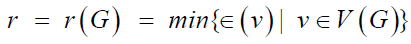. Also, the diameter of G, denoted by d(G), is the maximum distance between vertices of a graph G and hence 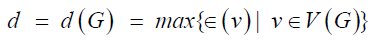. A vertex v with ∈_G(v)= r(G) is called a central vertex in G. A graph G with d(G) = r(G) is called a self-centered graph. A graph which contains only two non-central vertices is called almost self-centered graph [2] (ASC graph for short). Moreover, the eccentricity is also applied in chemical graph theory. There are several eccentricity-based topological indices, including the second Zagreb eccentricity index E2(G) [3] and eccentric connectivity index ∈^c (G) [4], of graphs G where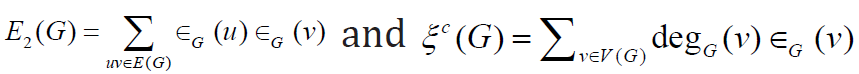

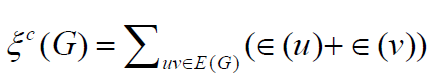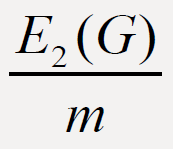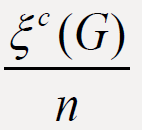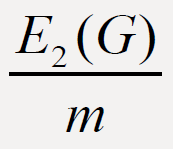In particular, we have or any graph G. In this paper we prove some comparison results between and of connected graphs G of order n with m edges. Main results In this we prove several results on the comparison between and 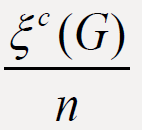of graphs G. Firstly we present two useful lemmas.

Lemma 2.1: [5] Let G be a connected graph of order n with maximum degree Δ . If Δ= n −1 then E₂(G) =ξ^c(G) .Otherwise, E₂(G) ≥ξ^c(G)with equality holds if and only if G is a 2-SC graph.

Lemma 2.1: [6] If u and v are two adjacent vertices of a connected graph G, then ∈(𝒰)−∈(𝒱) |≤1.

Denote by G_n(m; d) the set of connected graphs of order n with m edges and diameter d.

Theorem 2.3. Let G∈ζ(𝓂,𝒹) with n>5 and 𝒹≤2. Then 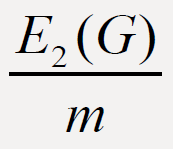<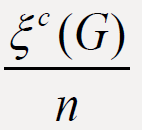. Proof. If d = 1, G∈ζ(𝓂,𝒹) contains a single graph Kn with 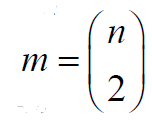and 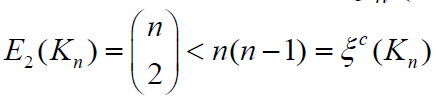. Then our result follows. Next it suffices to consider the case when d = 2. If G has maximum degree Δ = n −1by Lemma 2.1, we have E₂(G) <ξ^c(G) for any graph G∈ζ(𝓂,𝒹) .Moreover, we have 𝓂≥𝓃−1 If 𝓂=n-1, then G≅S_n with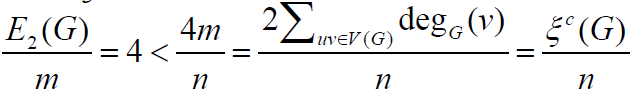 for any n ≥ 5. Moreover,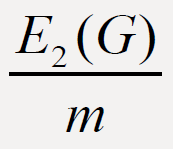<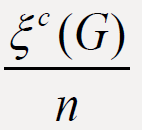holds clearly form ≥ n. If Δ ≤ n − 2 then G is a 2-SC graph. By Lemma 2.2, G is never a tree. Therefore m ≥ n with equality holding if and only if G ≅ C₄ or G ≅ C₅ . Consider that n > 5, m > n holds immediately. It follows that 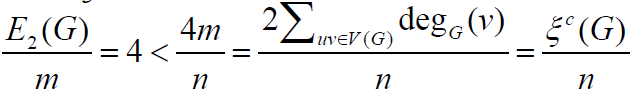. This completes the proof of the theorem.

In the following we consider the graphs G∈ζ(𝓂,𝒹) with diameter d ≥ 3.

Theorem 2.4: Let G∈ζ(𝓂,𝒹). with d ≥ 3, n > 5 be a tree or a unicyclic graph. Then 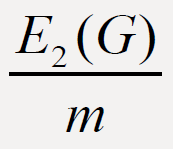>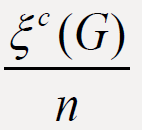Proof. If d ≥ 3, then Δ(G) ≤ n − 2 . From Lemma 2:1, we have E₂(G) <ξ^c(G). Note that m ≥ n for any tree or unicyclic graph G. Thus, it follows 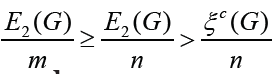. finishing the proof of the theorem. Next we consider the case

m > n. In the following theorem we give a sufficient condition for the graph G of order n with ≥ .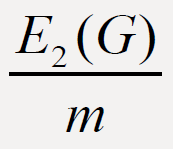

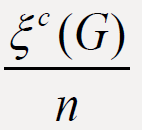Theorem 2.5. Let G∈ζ(𝓂,𝒹) with d ≥ 3, m = n + t and 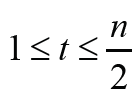. If r(G) ≥ 3, then ≥ ,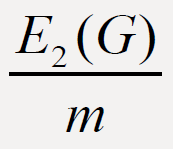

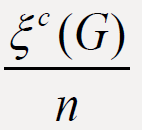Proof. Making a difference, we have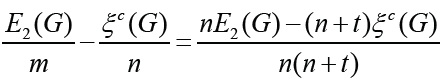

Set Δ₁= nE₂(G)−(n + t)ξ^c(G) . From Lemma 2.2, we have

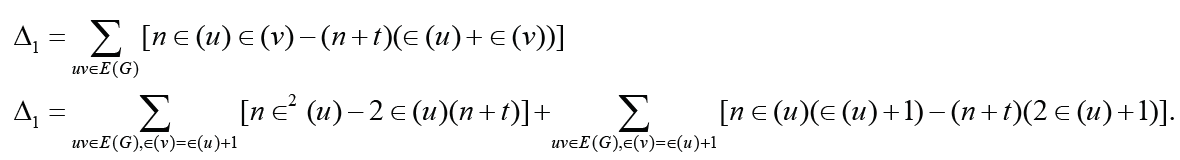
Since r(G) ≥3 and 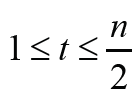, we have

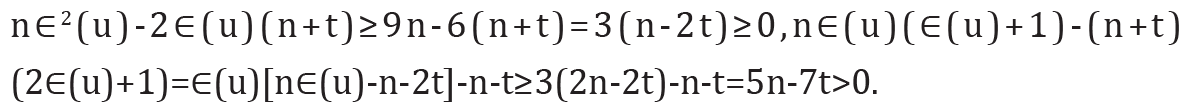
Therefore, Δ₁ ≥ 0 with equality holding if and only if ∈(𝓊) = 3for each vertex 𝓊∈V(G) that is, G is a self-centered graph with radius 3. This completes the proof of the theorem.

F or, G∈ζ(𝓂,𝒹) with d ≥ 3, r = 2 and 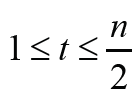considering that r(G)≤d(G)≤2r(G) we have d(G) = 3 or d(G) = 4. In this case, the value of Δ₁ may be negative, zero or positive. Let

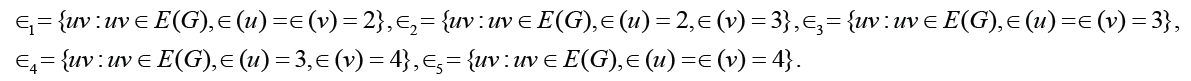
Denote by mi the cardinality of i∈{1, 2,3, 4,5}. Then

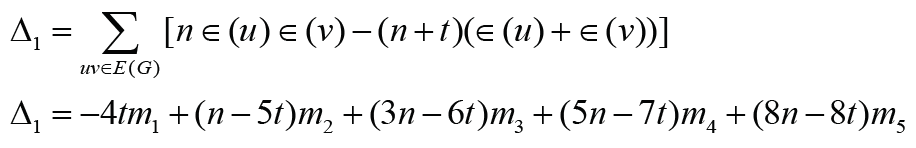
In the following result we present some comparison results for ASC graphs.

Theorem 2.6: Let G∈ζ(𝓂,𝒹) with d = 3, r = 2, m = n + t, t ≥ 1 where .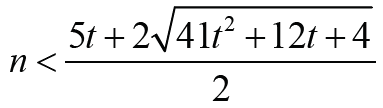

If G is an ASC graph, the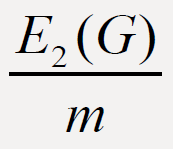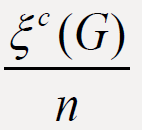n < Proof. If G is an ASC graph with d = 3, r = 2, from the structure of ASC graph, we have 𝓂₃≤ 𝓃 − 2,𝓂₃=0, that is, 1 𝓂 ≥ t + 2 . If 𝓃 ≤ 5t, clearly, we have Δ₁ ≤ 0 .For n >

5t, we have

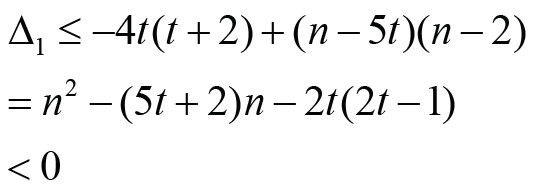
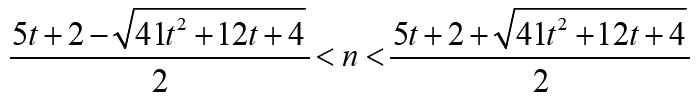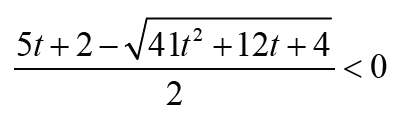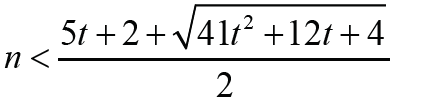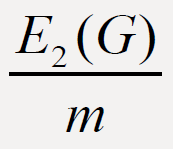holds if and only if Note thatThus Δ₁ < 0 is equivalent that with t ≥1. Therefore the result holds immediately. It is much interesting to search more generalized graphs G with different comparison results between and 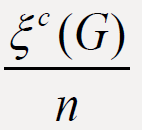which can be a topic for further research in the future.

References

1. JA Bondy, USR Murty (1976) Graph Theory with Applications. Macmillan Press, New York, USA, 1976.
2. S Klavzar, KP Narayankar, HB Walikar (2011) Almost self-centered graphs. Acta Math Sin (Engl Ser) 27(12): 2343-2350.
3. D Vukicevic, A Graovac (2010) Note on the comparison of the first and second normalized Zagreb eccentricity indices. Acta Chim Slov 57(3): 524-528.
4. V Sharma, R Goswami, AK Madan (1997) Eccentric connectivity index: A novel highly discriminating topolog-ical descriptor for structureproperty and structure-activity studies. J Chem Inf Comput Sci 37(2): 273-282.
5. KC Das (2016) Comparison between Zagreb eccentricity indices and the eccentric connectivity index, the second geometric-arithmetic index and the graovac-ghorbani index. Croat Chem Acta 89(4): 505-510.
6. M Behzad, JE Simpson (1976) Eccentric sequences and eccentric sets in graphs. Discrete Math 16(3) 187-193.